Simulating a Simple Pendulum in Python

One of the things that really made physics “click” for me was learning how to numerically simulate the systems I learned about in class. It’s one thing to write down the equations of motion for a certain problem – it’s another to actually visualize how they look like on a computer. It’s the missing link between the abstract and the real.

In this post, I’ll solve the problem of the simple pendulum – a ubiquitous toy problem in physics – and show how to simulate it on a computer. To understand the concepts in this post, you should have a basic knowledge of calculus and be familiar with programming logic.

The first step to simulating any sort of physical problem is to write out the analytic equations of motion. We will use the Lagrangian method, a particularly powerful way to analyze complex systems. Using it for the case of a simple pendulum is probably overkill, but I like the elegance in its approach. Our first step is to define our problem. A schematic of a simple pendulum is presented below:

The problem statement is then this: Find the equation of motion for a pendulum of length l and mass m. The Lagrangian approach to doing this is as follows:

Identify the generalized coordinate of the system, $q_i$ .
Write the Lagrangian, $L = T - V$ where $T$ is the kinetic energy and $V$ is the potential energy, in terms of the generalized coordinates $q_i$ .
The equations of motion for the system will then be given by the Euler-Lagrange equation, $\frac{\partial L}{\partial q_i}=\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{q_i}}\right)$ .

There will always be as many generalized coordinates as there are degrees of freedom in your system. The way I like to think about generalized coordinates is to imagine I’m on the phone with someone and I need to describe the state of my system to them. What is the minimum set of information I can tell them so that they can completely replicate my system? In the case of a simple pendulum, I could tell them the $x$ and $y$ positions of the mass, of course, but I could also just tell them the angle $\theta$ the pendulum makes with the vertical. One is fewer than two, and so the generalized coordinate for our simple pendulum is simply $\theta$ , corresponding to one degree of freedom.

The next step is to write out our energies in terms of the angle $\theta$ . The kinetic energy is easily written by remembering the relation $v=r\omega$ for circular motion and noting that in our case, the radius is simply the length of the pendulum:

$T = \frac{1}{2}mv^2 = \frac{1}{2}ml^2\dot{\theta}^2$

For the potential energy, we define our “zero” as when the mass is perfectly vertical, i.e. when $\theta=0$ . Then the “height” above the zero will just be $h=l-l\cos\theta$ , so the gravitational potential energy is:

$V = mgh = mgl(1-\cos\theta)$

We can now write the Lagrangian:

$L = T - V = \frac{1}{2}ml^2\dot{\theta}^2 -mgl(1-\cos\theta)$

and apply the Euler-Lagrange equation to get our equation of motion:

$\frac{\partial L}{\partial\theta}=\frac{d}{dt}\left(\frac{\partial L}{\partial\dot{\theta}}\right) \Rightarrow -mgl\sin\theta=ml^2\ddot{\theta} \\[10pt] -\frac{g}{l}\sin\theta = \ddot{\theta}$

Now we have our final analytic equation of motion. Note that the mass terms cancel out, suggesting that the motion of a pendulum is independent of its mass. At this stage, many introductory physics courses will take the small-angle approximation $\sin\theta \approx \theta$ in order to obtain the equation for simple harmonic motion, which can be solved analytically. Without this approximation, there is no analytic solution for the simple pendulum, but that won’t bother us here, since we are seeking to solve it numerically. We have a second-order ordinary differential equation, which we can write as two first-order ordinary differential equations:

$\frac{d\dot{\theta}}{dt}=-\frac{g}{l}\sin\theta \\[10pt] \frac{d\theta}{dt}=\dot{\theta}$

To numerically solve a system, the first step is discretizing it. The usual way to do this is by writing out the Taylor series for a continuous function and truncating it at some term. In our case, we want to find an approximation to $\theta(t)$ given our known initial condition $\theta(t_0)$ . Expanding $\theta(t)$ about $t=t_0$ , gives, to the first order:

$\theta(t) = \theta(t_0) + \dot{\theta}(t_0)(t-t_0) + O(t^2) \\[10pt]$

Rewriting, we have:

$\frac{\theta(t)-\theta(t_0)}{t-t_0}=\dot{\theta}(t_0)$

and plugging this into our system of differential equations, we get:

$\frac{\dot{\theta}(t)-\dot{\theta}(t_0)}{t-t_0}=-\frac{g}{l}\sin\theta \\[10pt] \frac{\theta(t)-\theta(t_0)}{t-t_0}=\dot{\theta}$

There is a question though – for the right hand side, at what time value should we compute $-\frac{g}{l}\sin\theta$ and $\dot{\theta}$ ? This is a non-trivial thing to decide, but for now we will compute these values at the past value $t_0$ , else we end up with multiple unknowns to solve for. Moving all our “knowns” to the right-hand side, we have:

$\dot{\theta}(t) = \dot{\theta}(t_0) + \left[-\frac{g}{l}\sin\theta(t_0)\right][t-t_0] \\[10pt] \theta(t) = \theta(t_0) + \dot{\theta}(t_0)[t-t_0]$

We now have a method for determining $\theta(t)$ and $\dot{\theta}(t)$ given the initial conditions $\theta(t_0)$ and $\dot{\theta}(t_0)$ where $t>t_0$ . Using $\verb|theta|$ and $\verb|omega|$ for $\theta(t)$ and $\dot{\theta}(t)$ and $\verb|theta_old|$ and $\verb|omega_old|$ for $\theta(t_0)$ and $\dot{\theta}(t_0)$ , we can translate this to programming logic as follows:

omega = omega_old - (g/l)*sin(theta_old)*tau
theta = theta_old + omega_old*tau

where we have defined $\tau=t-t_0$ to be a constant number. This is our update equation, which we will loop through every time we want to “step forward” in time to obtain a future value for $\theta(t)$ . The only things we need to specify ahead of time, aside from the constants, are the initial conditions. The relevant code, written in Python, looks like this:


import numpy as np
from math import *

def simplePendulumSimulation(theta0,omega0,tau,m,g,l,
                             numSteps,plotFlag):

    # initialize vectors

    time_vec = [0]*numSteps
    theta_vec = [0]*numSteps
    omega_vec = [0]*numSteps

    # set initial conditions

    theta = theta0
    omega = omega0
    time = 0

    # begin time-stepping

    for i in range(0,numSteps):
        omega_old = omega
        theta_old = theta
        # update the values
        omega = omega_old - (g/l)*sin(theta_old)*tau
        theta = theta_old + omega_old*tau
        # record the values
        time_vec[i] = tau*i
        theta_vec[i] = theta
        omega_vec[i] = omega

Running this code for initial conditions $\theta(0)=1$ and $\dot{\theta}(0) = 0$ , we immediately see a problem, though:

The total energy is increasing without bound! In other words, the energy of the system is not conserved. You can see this by the ever-increasing displacement of our pendulum, which paradoxically swings higher and higher with every rotation. The problem lies in our crude first-order approximation we made earlier when discretizing our solution. After all, our equation of motion is nonlinear, making linear approximations especially ineffective at solving it. In lieu of using higher-order methods, we can just apply a simple modification called the Euler-Cromer method, which is guaranteed to conserve energy. We simply use the updated value of the angular velocity as it becomes available:

omega = omega_old - (g/l)*sin(theta_old)*tau
theta = theta_old + omega*tau

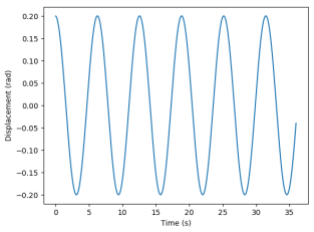
You can see that $\verb|omega_old|$ in the second line has been simply changed to $\verb|omega|$ . Running the simulation again, we get the results:

The pendulum now properly returns to its initial displacement after each cycle. We see that although the total energy still fluctuates a bit (due to our first-order approximation), it is now properly bounded. To reduce the fluctuations in energy, we can simply reduce the time stepThe Python script to perform the simulation using the Euler-Cromer method and generate the images is given here: pendulum.py

Tags: computational, mechanics, pendulum, physics, python, simulation

2 comments

Renzo Shredder · August 25, 2018 - 6:16 am · Reply→

Awesome post. Can’t wait to go through the rest of your site!

LikeLike
cloud11665 · November 12, 2022 - 6:15 pm · Reply→

Thanks for bringing up the Euler-Cromer method, it was the last piece of the puzzle that I was missing. Very nice post!

LikeLike

Jeremy Kao

Simulating a Simple Pendulum in Python

2 comments

Leave a Reply Cancel reply

Jeremy Kao

Simulating a Simple Pendulum in Python

Share this:

Like this:

2 comments

Leave a Reply Cancel reply